インデックス長期投資を行う際に投資家が最も気になることの一つは過去の年間利回りだと思います。
過去の結果がそのまま未来に当てはまるわけではないですが、長期的なデータがあれば過去を通して未来を概ね予測することは可能です。
例えば、米国株式市場は配当再投資条件で実質トータルリターンが過去200年に渡り6.7%程度でした。
このことから、米国株式インデックス投資を長期的に行おうと考える人は多いと思いますが、上記の6.7%というのは一括投資を行った場合の長期的なリターンとなります。
では、積立投資を行う場合、投資総元本とその平均リターンはどのようになるでしょうか?
私は積立投資を実践しておりますが、そのパフォーマンスについて正確に書かれた情報は見たことがなく、調査するのもめんどくさかったので自分で数式により理論式を求めてみました。
数式と言うと拒絶反応が出る方もいらっしゃるかもしれませんが、図を交えて説明しておりますし、式からわかる結論自体は難しくないので(重要なのは式ではなく結論ですし)、お気軽にお読みいただければと思います。
積立投資の利回り算出理論式
積立投資の利回り式を求める前に、仮定を二つ置きます。
ここで、利回りのbとは%ではなく割合です。つまり、利回り5%の商品であればb=0.05と表されます。
さて、準備が整ったので、積立投資のパフォーマンス理論式を以下に示します。
はい、以上です!Excelで各自この数式をご活用ください!
と言っても芸が無いので、各期待利回りに対する積立投資の年間幾何平均リターンをグラフで示してみます。
積立投資のパフォーマンス
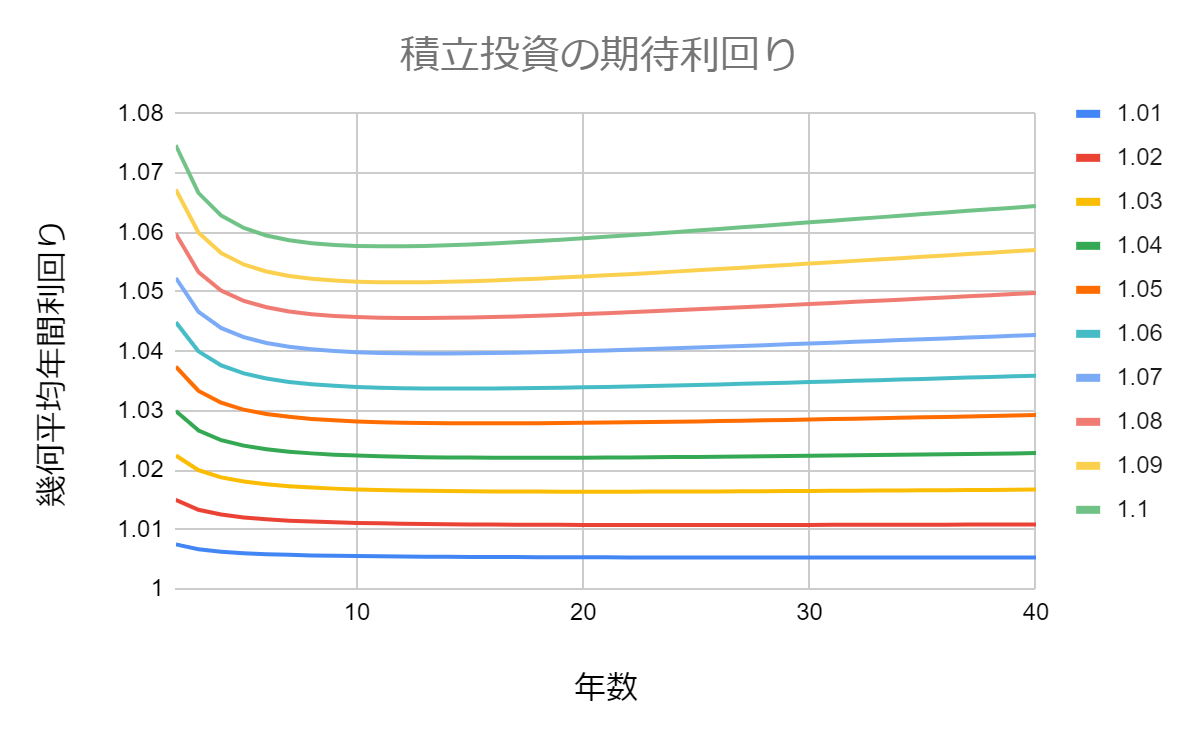
前段で求めた積立投資の利回りの理論値を用いて、総投資元本に対する年間幾何平均利回りの時間経過をグラフで示します。
条件としては以下となります。
ちょっと上の日本語が紛らわしくてわかりにくいかもしれませんが、要は年間期待利回りxの商品に毎年a万円積み立てたときの経過年数毎の幾何平均での年間利回りを、x=1.01、1.02、1.03、…、1.1の条件で色を分けてプロットした図です。
年間期待利回りが1%や2%と低い条件の場合は、積立投資だと投資元本に対して約半分の幾何平均利回りのまま推移します。
一方、年間期待利回りが7%以上と高い条件の場合は、複利の効果がじわじわ効いてくるため、積立投資では投資元本に対して半分以上の利回りで底打ちし、10から15年を超えると幾何平均利回りが上昇していくことがわかります。
例えば配当再投資条件で実質年間期待利回り1.07倍の米国株式インデックスを積み立てる場合は、毎年増えていく総元本an万円に対する期待利回りは1.04%程度となることがグラフの薄いブルーの線からわかります。
以上から、結論としては、毎年一定額の積立投資でざっくり利益を計算したければ、総元本に対して商品の期待利回りの半分の利回りを保守的に想定しておけばOKだということがわかりました。
理論式の導出
この節は、数学が好きな人かもしくは興味がある人だけお読みいただき、それ以外の人は「まとめ」にスキップしてください。(とはいっても簡単な高校数学レベルです)
理論式の導出は上の写真の通りです。
一年目の頭にa万円投資した場合、期待倍率をx(利回り5%ならx=1.05)とおくと1年後の期待収支はaxとなります。
二年目は、ax+aという元本に対してxの利回りが掛けられるのでax(x+1)となります。
これを続けていくと、n年後の運用資金はax(xn-1+xn-2+…+x+1)となります。
これを整理すると、n年後の期待運用資金はax(xn-1)/(x-1)となり、幾何平均利回りはこの期待運用資金を元本anで割ってからn乗根をとって[x(xn-1)/{n(x-1)}](1/n)となります。
(xの代わりにbを使えば先述の式となります)
まとめ
積立投資の期待利回りの理論式を知りたかったので、商品の年間期待利回り通りのパフォーマンスで右肩上がりに資産が増加する場合を仮定して導出してみました。
その結果は以下です。
この結果を基に、各利率の商品に対して年間幾何平均利回りをシミュレーションしてみたところ、毎年定額の積立投資では投資総元本に対してざっくりと商品の年間利率の半分を想定しておけばよさそうだということがわかりました。
毎年一定の利率で右肩上がりに増加すると仮定した場合は、同額を一括投資した場合と比べると、利回りが年間ベースで半分に落ちるということですから、一括投資の優位性がよくわかります。
とはいえ、株式市場の場合には実際は乱高下しながら長期的に平均利回りに収斂するので上記のシミュレーション通りにはなりませんが、一定の目安にはなるかと思います。私の場合は、一括投資の合理性を理解しつつも史上最高値付近での一括投資は避けたいので、3年ほどかけて現在の大きすぎるキャッシュポジションを株式インデックスに変換していこうとしております。
積立投資についてより深く学んでいきたいと言う方には「積立投資のすべて」という書籍がおすすめです。下落相場に対して積立投資が如何に強いかがよくわかる隠れた名著です。
一括投資をした場合の長期パフォーマンスとしては、S&P500の過去の期待リターンとリスクから、大量に乱数を振って(サイコロを転がすようなものです)長期投資の成績の確率分布を計算する「モンテカルロシミュレーション」も以下の記事で行っておりますので、お読みいただけると幸いです。






コメント